AMM 三角：流动性提供者、期权和 AMM 「翻译」

编译：Antalpha Labs

今天，我们与 Panoptic 的 Guillaume Lambert 以及 Bancor / Carbon 的 Mark Richardson 进行了一次非常有趣的讨论，主题涉及提供流动性（lp）、交易和自动做市商（AMM）。我想在这里简要地提出一些我已经思考了一段时间的想法，这些想法相互关联，但是我也不是非常确定他们如何应用。

译注：Guillaume Lambert 是在 twitter 和 medium 以及 uniswap 社区非常活跃的教授，有自己的项目 Panoptic ，对 lp 与期权的相关讨论也非常多。

我想描述的关键概念，是我想称之为"AMM三角形"的东西，一方面它代表了AMM（自动做市商）中不同参与者之间的关系（流动性提供者和套利者），另一方面是期权交易者（特别是对冲期权买家）。让我们首先从这个三角形开始：

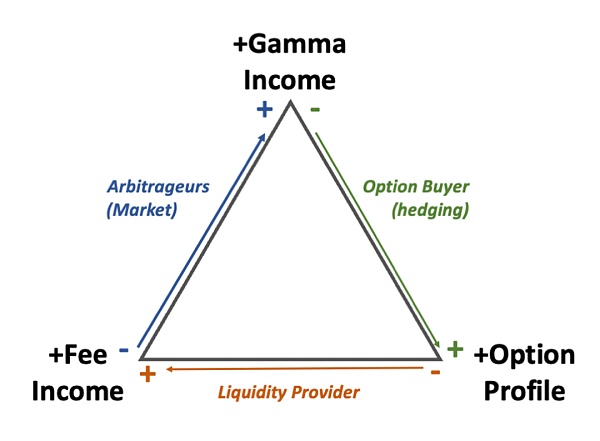
AMM 三角

这个概念代表了与 AMM（自动做市商）头寸相关的三个价值流（暂时没有更好的词来描述）：

1. 流动性提供者每次在 AMM 上进行交易时收到的手续费

2. 与无常损失相对应的期权组合，这里考虑的是拥有一个看涨期权（与链接^[1]中所述的平方根配置相匹配）的投资组合。

3. 与期权配置对冲以及 AMM 头寸再平衡相对应的 Gamma 收入

译注：这里的开平方指的是，例如 eth -u 的 uniswap 头寸的价值和 eth-u 价格关系是开平方的关系。这个会在后续的文章单独补充说明。call 期权也是广义期权。

我们现在确定了三种典型的市场参与者，每一种都占据了三角形的一条边，这意味着他们在相应的顶点上是空头，而在其他地方是多头。更详细地说：

1. 流动性提供者获得费用收入，但是做空对应期权组合，后者包含无常损失^[2]和相对应的平方根期权收益^[3]

2. 套利者是交易手续费的收入的空头，但是他们能获得与无常损失相对应的 gamma 收入

3. 期权交易者长期持有期权组合并对其进行对冲，因此对 gamma 收入持有空头仓位。

我在theammbook.org^[4]论文的AMMs和金融衍生品^[5]章节中详细讨论了这些主题，这里只给出高层次的直觉。

流动性提供者的处境：AMM 在设计上给予其手续费，k=x*y 的恒定积的 AMM 的无常损失损失对应的平方根期权对应已经研究的差不多了，同样，集中流动性的期权特性也对应于流动性范围内的期权组合。

套利者是交易手续费的空头——这就是你在 AMM 上交易时要支付的费用。可能不完全明显的是，他们还是 gamma 的多头。要理解这一点，关键的信息是，套利者的交易使价格从 P0 移动到 P1，平均成交价格是几何平均 sqrt(P0*P1)。这意味着什么呢？让我们使用标准的假设，没有最终客户，市场深度大且流动性好，套利者在该市场和 AMM 之间进行交易。在这种情况下，众所周知，AMMs 将被持续套利，使其边际价格对应于市场价格。那么，当价格从 P0 移动到 P1 并返回时会发生什么呢？正如我们之前看到的，AMM 以相同的价格买入和卖出，即几何平均数。然而，套利者已经以 P0 的价格买入，并以 P1 的价格卖出，即捕获了完整的市场移动——这就是他们的“gamma 收入”，并且可以轻易地证明，这个伽马确实对应于 AMMs 的“暂时性损失”收益概况。

对于期权交易者来说，一样地众所周知：如果交易者持有一个期权概况并进行 delta 对冲，那么——当然只在理想的 Black Scholes 世界中——他们的 delta 对冲成本正好是他们在到期时的收益。

这个模型有一些基本的缺陷需要了解，部分原因是套利者和交易者都是在非常理想化的市场环境中被讨论的，这其中存在一些基本的问题，例如：

• 如果有一个深度和流动性都很好的市场，我们为什么需要 AMMs？为什么人们不都在那个深度和流动性好的市场上交易？

• 世界并不是一个 Black Scholes 世界，delta 对冲并不是一个完美的复制策略

• 套利者有选择不交易的权利，所以他们只会在他们的 gamma 收入高于他们支付的费用时参与；伽马等同于期权到期收益，因此费用永远不能补偿暂时性损失

现实是，市场微观结构比 Black Scholes 和深度-流动市场假设所暗示的要丰富得多，在现实世界中，每个人都有他们的位置。然而——在我看来，AMM 三角形给出了一个很好的结构性指示，说明了这些不同方面是如何相互关联的，以及如何结合它们来提取某些特定的流动性，特别是与期权相关的流动性。