区块链NFT投资,BTC/USDT/CGPAY,虚拟加密货币交易行情分析平台
慢雾:Ed25519 实现原理与可延展性问题
Ed25519 是一个基于椭圆曲线的数字签名算法,它高效,安全且应用广泛。TLS 1.3, SSH, Tor, ZCash, WhatsApp 和 Signal 中都使用了它。本文主要讲解以下几点:
- 介绍一点群论知识,目的是让大家对 Ed25519 和其可延展性问题的原理有一种直觉。若想深入理解,还需参考其他资料;
- 针对 rust 库 ed25519-dalek 的 1.0.1 版本讲解 ed25519 的实现;
- 针对该库的延展性问题做出解释。
群的定义与性质
群论是抽象代数研究的内容,但抽象代数的一些思想是程序员非常熟悉的。面向对象中的继承就是一个很好的例子,我们都知道子类继承了父类后,就能使用父类中定义的方法。可以将抽象代数理解为对一个抽象的数据结构定义了一些性质,由这些性质推导出来的定理对于所有的子类都成立。
沿用刚刚的比喻,来看看群(group)这个数据结构是如何定义的。由此可以推出许多有意思的定理:举几个例子:
被一笔带过的群论术语
拉格朗日定理
现在介绍一个非常有意思的定理,这个定理的推导在文末引用的视频中。“群的阶能被子群的阶整除。”为什么说这个定理有意思呢,不仅仅因为它的证明过程串起了刚刚介绍的许多知识,还因为下面的结论:
Ed25519 的实现
现在我们来讲 Ed25519,它是 EdDSA 算法的其中一种。EdDSA 有 11 个参数,这些参数的具体选择对于算法的安全和性能有很大的影响。另外,值得一提的是这套算法用到了一个叫 Curve25519的椭圆曲线。对于椭圆曲线,我们只需知道,它上边有很多很多点,这些点相加能得到新的点,新的点还是在曲线上。这些点和这个加法能形成一个群。注意这里的椭圆曲线加法是有特殊定义的。
我们约定如下记法:
这是个交互式的算法,但是没关系,有一个技巧叫做 the Fiat – Shamir heuristic,它可以把任意的交互式算法转化成非交互式的算法。最终我们会用非交互式算法。
数字签名算法都会给我们如下 API:

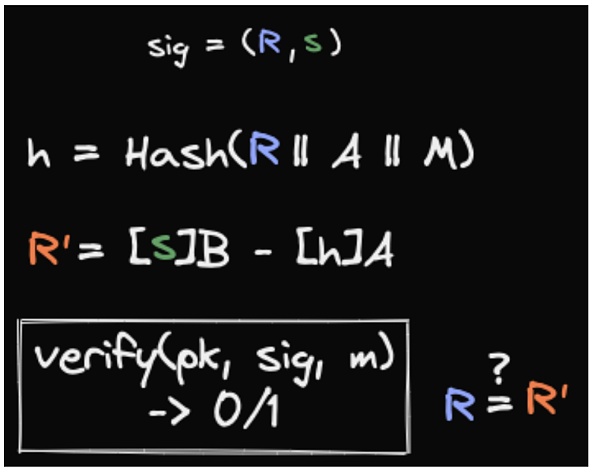

可延展性问题
密码学算法的实现和使用都有非常多要注意的地方。当我们说一个数字签名算法是安全的,一般指的是即使在攻击者能够获得任意消息的签名(Chosen Message Attack)的情况下,攻击者仍然不能伪造签名。Ed25519 满足这个性质,但不代表 Ed25519 是绝对安全的。在原始的论文中也提到,可延展性问题是可以接受的,且原始的算法就有这个问题。

相关文章
- 2025 加密钱包市场深度测评:不止于存储,Web3 时...
- [限时一周]入款限时加码0.5%,18周年庆暖身倒数,...
- NFT市场从投机热潮到数位基础设施的NFT转型崛起
- Web5白皮书详解:去中心化网络平台的未来愿景与技...
- 探索Web3、Web4和Web5引人入胜的三大浪潮
- 揭开Web3技术的误解,Web3未来挑战与展望
- 你知道2025年比特币挖矿需要准备什么吗?
- 购宝钱包G币充值三千粽粽有赏活动
- 比特币涨势在97,000美元时出现抛售,Cardano领涨市...
- Toobit是一个安全的加密货币交易所吗?
- 2025最新虚拟货币怎么玩?新手如何安全入场与获利...
- 7种2025年热门加密货币最值得购买的加密货币
- 90%人不知道的ABpay爱博钱包图文教程使用技巧!安...
- 波币短线交易全攻略:如何在波币市场中获利掌握市...
- 夜间指定电子钱包USDT入款获奖金16,888
- EcoChain碳负货币引领绿色金融的未来


 BTC
BTC ETH
ETH USDT
USDT XRP
XRP BNB
BNB SOL
SOL USDC
USDC TRX
TRX DOGE
DOGE STETH
STETH














